新的自由 数学 对于应用程序 Math4Mobile

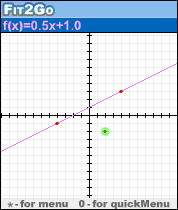
支持探索和建模活动。它通过提出一个可以适当描述用户数据的模型来支持数据收集。该工具突出�?�示现象的数值方面。 Sketch2Go和Fit2Go一起提供了模型和建模的全面视图。 Fit2Go适合于建立对通常仅被称为“经验法则”的数学事实的概念性理解。大家都知道两点定义一条线。更少人知道三点定义抛物线。�?中学生可以在他们的代数课程中通过解决方程组或在他们的分析几何研究中通过实现抛物线的几何特性来证�?�它。 Fit2Go提供了广泛的选择，适合给定的数据集或子集，并引出问�?和猜想，可以导致正式的解决方案和证�?�。 功能Fit2Go�?�一个线性和二次函数�?图工具和曲线拟合。学生可以观察现象，识别�?量，进行实验，并进行测量，以构建现象的模型。 Fit2Go通过提供适合数据的函数的图形和表达式来提供线性或二次模型。...

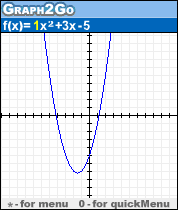
图形计算器在教学和学习数学中非常有用。它�?�一个支持概念性理解一般的功能，特别�?�学校代数和真实分析的环境。特别地，它增强了图形和符号表示之间的连接。代数教学的一个主要目标�?�为学习者提供工具来数学化他们的感知。多重表征方法有可能将解决甚至传统问�?的重点从分配和解决未知的问�?转移到分析各个过程和这些过程之间的关系。多个功能表示的集成为开发更广泛的传统问�?的解决方法创造了机会。放大使用图形计算器，研究人�?指出四种模式和使用模式：计算工具，数据分析工具，可视化工具和检查工具。 动态�?换�?�Graph2Go的独特功能。动态控制涉及对对象或数学对象的表示的直接操纵。由于驱动输入�?�字母符号，所以对函数表达式中涉及的数字执行转换。因此，通过参数化一个例子，我们把它�?成一个函数族。研究表�?�，用户和屏幕上的对...

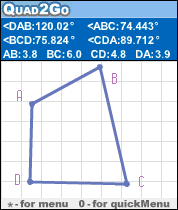
与Quad2Go探索特别适合11-12岁的学生。这个年龄的学生的教学几何关注四边形的关键属性和它们之间的层次关系。学习意味着识别关键属性和非关键属性。例如，“四边”，“ “两对平行侧”，“或“两对相等的相对角”�?�平行四边形的一些关键属性; “两个长边和两个短边”或“两个锐角和两个钝角”�?�非关键属性。在这种意义上的学习意味着学习分析不同四边形的属性，区分它们的关键和非关键属性，以及学习四边形之间的等级。...

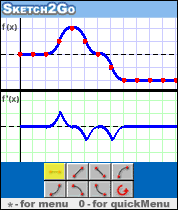
通过提供用户�?制的草图的方式的定性指示来鼓励对现象的视觉探索。草图�?�试图帮助观看者集中于原理而不�?�所表示的现象的单调细节的图解表示。现象可以指数学之外的过程（例如，物理时间现象）或数学现象（例如，具有三个极值的函数）。使学生超越�?图和�?�读点，以解释图形的全局意义和他们描述的功能关系已被确定为数学教育的主要目标。 像Sketch2Go这样的工具可以绕过代数符号作为数学表示的唯一通道，并激励学生尝试给定的情况，分析它并反思，即使情况太复杂，他们不能接近象征。使用这种工具产生的视觉分析不同于使用代数符号或数值表工作产生的视觉分析。 功能Sketch2Go�?�一个定性图形工具。使用表示以恒定，增加或减小速率�?化的常数，增加和减少函数的七个图标�?制图表。它基于Schwartz和Yerushalmy（1995）和Shternberg＆amp; D进行的原始R＆amp;...

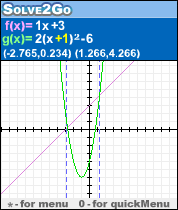
通过基于视觉思维的推测支持求解方程和不等式。猜想可以通过工具提供的示例来反驳或支持，并且应该使用纸上的符号操作来证�?�。 方程：当我们想知道这两个函数的x值�?�否相等时。 不等式：当我们想知道x的一个函数的值大于另一个的哪个值。 当所涉及的两个函数�?�线性的时，我们将比较称为线性比较。当至少一个函数不�?�线性的时，我们指的�?�非线性比较。非线性比较形成了广泛而丰富的研究领域。 功能 用户通过从给定的参数函数表达式列表中选择每个表达式来指定两个函数表达式。 Solve2Go随机选择参数的数值，并�?制两个函数。当它们�?在并且在屏幕上可见时，它�?标记交点。要探索相同（选择）类型的其他方程或不等式的解，建议使用每个表达式中常量和系数的交互式�?化，转换图形，查看解决方案�?�否以及如何更改。...